Introduction

Hi, I'm Raul, this is my first post on my blog, where I'll share a little of what I know, during the past year I decided to strengthen my knowledge of data structures and algorithms.

Time complexity

For this I would like to start by teaching how the efficiency of an algorithm can be measured, we could think that the best way to compare two blocks of code would be by measuring the execution time of both, but in practice This may vary due to several factors:

• Computer specifications
• The availability of computer resources

To do this, it's better to measure performance based on time complexity , which is defined as:

Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, assuming that each elementary operation requires a fixed amount of time.

#Big O notation

The Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular or infinite value.

Surely you have heard of Big O, it is the most used notation in programming to analyze algorithms, Without going into too much detail, we can define the Big O notation of an algorithm through the sum of operations it performs, below the most common:

• Operation O(1): Access an index of an array, perform a sum, etc.
• Operation O(log N): Perform binary search within an array of size N.
• Operation O(N): Access each element of an array of size N.
• Operation O(NlogN): Perform a sort using Merge Sort.
• Operation O(N²): Perform a bubble or Quicksort sort in the worst case.
• Operation O(N!): Generate all possible permutations of N.

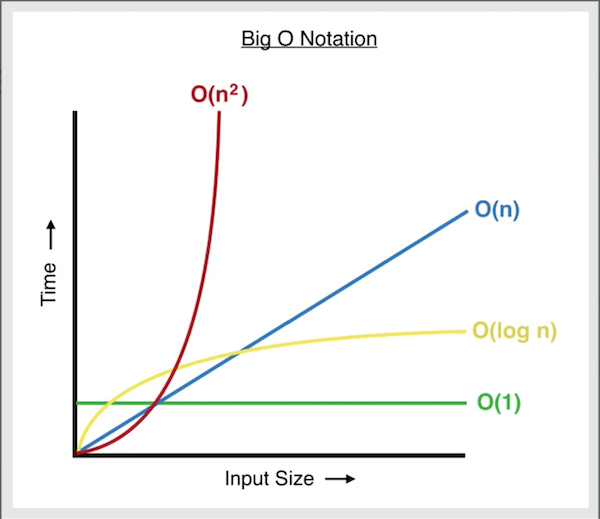Figure 1. Big O trading chart.

Example

Next we are going to evaluate a simple but written algorithm in different ways.

In mathematics, the Fibonacci sequence or series is the following infinite sequence of natural numbers: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597 ...

def getNthFib(n):
    if n == 2:
        return 1
    elif n == 1:
        return 0
    
    return getNthFib(n-1) + getNthFib(n-2)
  

Time complexity: 2^n, space complexity O(1)

def getNthFib(n, memo = {1: 0, 2: 1}):
    if n in memo:
        return memo[n]
    memo[n] = getNthFib(n-1) + getNthFib(n-2)
    return memo[n]

Time complexity: O(n), space complexity O(n)

def getNthFib(n, memo = {1: 0, 2: 1}):
    lastResults = [0, 1]
    iteration = 3
    while iteration <= n:
        next = lastResults[0] + lastResults[1]
        lastResults[0] = lastResults[1]
        lastResults[1] = next
        
        iteration += 1
    return lastResults[1] if n > 1 else lastResults[0]

Time complexity: O(n), space complexity O(1)

Conclusion

Without a doubt, it is important to analyze each of our algorithms, specifically if we work with large amounts of data, remember that not all implementations are the same.

So far I write today, I will try to write a weekly publication.